The Math Circle is no longer active, but has been replaced by Blue Ridge Boost! Coding classes, camps, and math tutoring.
21 May 2020: Encountering the Uncountable
Is there anything bigger than the Natural Numbers?
Slides (with annotations): PPTX
19 May 2020: Infinity and Beyond
What are numbers for, and how many do we have?
Slides (with annotations): PPTX
11 May 2020: Maryam Mirzakhani Movie
Home screening of Secrets of the Surface: The Mathematical Vision of Maryam Mirzakhani.
5 May 2020: Pythagorean Theorem
What is a mathematical proof?
Slides (includes videos): PPTX
28 April 2020: Marvelous Measurements
How can we measure lengths and areas?
31 May 2019: Math Restaurant

15 March 2019: Pi-Day
How big is a pie with unit radius?

|

|

|

|

|

|
4 January 2019: Pizza Slicing

|

|

|
What is the maximum number of slices one can make using straight line cuts?
We figured out that you can make 7 pieces with 3 cuts, 11 pieces with 4 cuts, and 16 pieces with 5 cuts!
Yummm…that’s a lot of pizza slices. (Three-dimensional cake cutting is reserved for a more advanced math circle.)
October – December 2018: Math Olympiad Problems
6 October 2018: Kodables
22 September 2018: Pythagorean Magnets

|

|

|

|

|
14 September 2018: Capture 5
Game from Ms. Fox’s class.
24 August 2018: Olympiad 5
(From Math Olympiad Contest Problems for Elementary and Middle Schools, Vol. 1)
Olympiad 5: problems 1, 5.
9 August 2018: Olympiad 4
(From Math Olympiad Contest Problems for Elementary and Middle Schools, Vol. 1)
Olympiad 4: problems 1, 3.
2 August 2018: Olympiad 2
(From Math Olympiad Contest Problems for Elementary and Middle Schools, Vol. 1)
Olympiad 2: problems 1, 3, 4, 5.
26 July 2018: Cubetto Challenges
Some challenges with the Cubetto Toy Robot:
-
What does this block do?
- Easy for most, but interesting for the “Cream” blocks (which make the subsequent behavioral block have the opposite behavior, but can be used with multiple cream blocks, etc.), “Black” block (picks a random behavior), and “Blue” block (calls the subroutine)
-
Make the robot travel furthest
- Some interesting attempts, first using up all the Forward (Green) blocks and then using Cream-Purple-Cream-Purple (opposite-reverse to go forward) as the subrouting, before figuring out that it is best to use 4 Green in the subroutine, and all the “Blue"s to call it.
- Then, understanding the “Blue” / “Green” “Blue” three-block move forever program.
-
Make the most lights blink at once
- Can put 4 Creams + Blue + subroutine lbock to make 6 blink. Is there a way to get 7?
12 July 2018: Visual Cryptography
Making secret pictures using visual cryptography.
5 July 2018: Jefferson Wheel Ciphers
22 June 2018: Geometry
Finished the geometry problems (Geometry Axiom Problems (PDF)).
14 June 2018: Straightedge and Compass
We practiced using the ruler and compass on creative drawing. We used the ruler and compass to draw a perpendicular on a given line and to draw a square.
7 June 2018: Problems about Points and Lines
Geometry Axiom Problems (PDF)
25 May 2018: Geometry from Axioms
Introduction to Euclidean Geometry Definitions and Axioms (PDF)

18 May 2018: Sharing Marbles
(From the Math Olympiad Contest Problems, Volume 1)
A set of marbles can be divided in equal shares among 2, 3, 4, 5, or 6 children with no marbles left over. What is the least number of marbles the set could have?
We also tried the same problem with numbers 3, 5, 7.
Since our crowd does not know multiplication yet, but knows skip count and divisibility criteria, we found two ways to solve the problem. The number we’re looking for is the first common one in the number chains of the 4, 5, 6. The other way is to write down the number chain for 7 and use the divisibility criteria for 3 and 5 that we already know to find the number.
4 May 2018: Divisibility
We can tell if a number is divisible by 3 by summing its digits and seeing if the result is divisible by 3!
The works because 10 = (3 * 3) + 1. So, each multiple of 10 that is added, is adding 1 modulo 3.
28 April 2018: Puzzling Pennies
(From the Math Olympiad Contest Problems, Volume 1) From a pile of 100 pennies, 100 nickels, and 100 dimes, select 21 coins that have a total value of exactly $1.00. In your selection you must also use at least one coin of each type. How many couns of each of the three types should be selected?
21 April 2018: Coin Puzzle
(From the Math Olympiad Contest Problems, Volume 1) I have 30 coins consisting of nickels and quarters. The total value of the coins is $4.10. How many of each kind do I have?
The tower below is made up of five horizontal layers of cubes with no gaps. How many individual cubes are in the tower?

15 April 2018: Radix Sorting
We split numbers 1 – 100 in buckets by the first digit and the used various sorting algorithms, such as quicksort, insert and merge sort to sort each bucket.
7 April 2018: Sorting Algorithms
We did bubblesort (which took a lot of persistence by finished successfully!) and quicksort.

|

|

|
23 March 2018: Fusing Dots
Fusing Dots machine (from the Berkeley Math Circle): [PDF]
16 March 2018: Smullyan’s Criminals
Smullyan’s Criminals problems from the Berkeley Math Circle: [PDF]
9 March 2018: Boolean Island
We did some puzzles based on the Knights and Knaves from Raymond Smullyan’s What is the Name of this Book?: [PDF]
The last puzzle was to make up your own puzzle about the Boolies.
2 March 2018: Water Rainbows
We can make colored water with different densities by mixing in different amounts of sugar. Then, we can make a separated rainbow of different colored water in a straw!

|

|

|

|
23 February 2018: Tree Adding

|
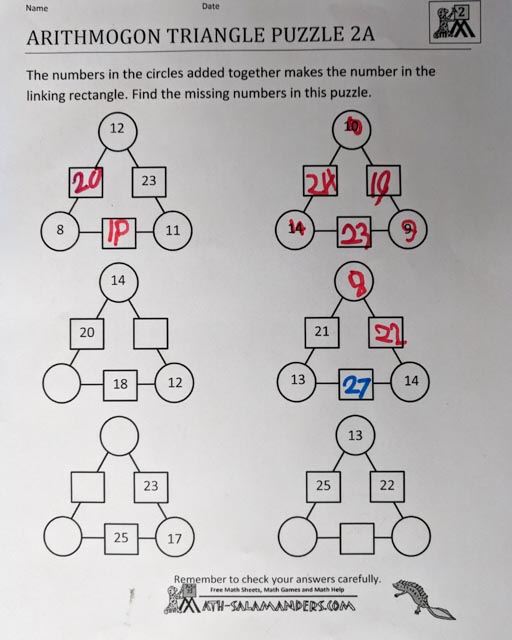 |
||

|

|

|
|
8 December 2017: Making Octahedrons with Stawbees

|

|

|

|
1 December 2017: Out with the Onion
From Martin Gardner’s My Best Mathematical and Logic Puzzles (55): Move two matches, to remake a class, but with the cherry outside.
Dissection Dilemma (57): divide a square into five parts, all identical in size and shape.
24 November 2017: Apples and Sticks
-
Given three piles of 11, 7, and 6 stones, respectively. You can only move from one pile to another exactly as many stones are at the destination. In three moves, obtain three piles of 8 stones. (From The Moscow Puzzles, by Boris A Kordemsky)
First Dorina and Anya had a solution in four moves that starts with moving from the 11 stone pile to the 6 stone pile: (11,7,6), (5,7,12),(10,2,12),(8,4,12),(8,8,8). After a few tries, they figured out the three moves solution: (11,7,6), (4,14,6), (4,8,12), (8,8,8).
-
Five apples are in a basket. How do you divide them among five girls so that each girl gets and apple, but one apple remains in the basket. (From The Moscow Puzzles, by Boris A Kordemsky) This was quite confusing, until David brought a prop. Then it seemed silly.
-
Take 4 sticks of equal length and 4 more of equal length twice the first length. Use all 8 to make 3 squares of equal size. It’s acceptable to cross two long sticks. This was a pretty hard one. It took a while, but we finally did it.
17 November 2017: Relatively Prime
Everyone knows number lines (and number chains), but now its time for number rings!

|

|
If two numbers, n and k are relatively prime, we will touch every number in the modulo number ring for n going by multiples of k. Dorina picked 25 and 6, Anya picked 12 and 5, Charlotte picked 12 and 3 (not relatively prime, so doesn’t touch every number), and Madelyn picked a number too big to finish.
(This is what we covered in cs2102: Discrete Mathematics the day before.)
10 November 2017: Perimeters and Areas
With 12 sticks, make a closed polygon with the largest area. With 12 sticks, make a closed polygon with the smallest integral area.
3 November 2017: Pentagram

With enough paper and colors we counted all 35 triangles!
28 October 2017: Puzzling Pentagrams
Moving Checkers
Place six checkers on a table in a row, alternating them black, white, black, white, block white. Move the checkers so that all the white one will end on the left, followed by the black ones. The checkers must be moved in pairs, taking two adjacent at a time, without disturbing the order, and sliding them to a vacant place. Only three such moves are necessary. (From The Moscow Puzzles, by Boris A Kordemsky)
This was a pretty successful problem. The girls enjoyed moving the stones around and find a solution.
Count!
How many different triangles are there in the pentagram figure? (From The Moscow Puzzles, by Boris A Kordemsky)
We were able to identify all the types of triangles, but we didn’t find a successful strategy for counting all 35 triangles, despite several persistent efforts from the girls.
21 October 2017: Scrambled Box Tops
Some more variations on the puzzle from 13 October.
13 October 2017: Stick Puzzles
-
Use 12 sticks to form polygons with integral areas. The entire length of the stick must be used with no overlapping, but more than one stick may be used for an edge. Assuming the sticks have unit length, what how many area units does your polygon have?
The solutions we had were: square with area 9 and rectangle with area 8. The challenge to get back to later: form a polygon of exactly four square units. (From My Best Mathematical and Logic Puzzels by Martin Gardner, Puzzle 14, “The 12 Matches”.)
-
Scrambled Box Tops
Imagine that you have three boxes, one containing two black marbles, one containing two white marbles, and the third, one black marble and one white marble. The boxes were labeled for their contents but someone has switched the labels so that every box in now incorrectly labeled. You are allowed to take one marble at a time out of any box, without looking inside, and by this process of sampling you are to determine the contents of all three boxes. What is the smallest number of drawing needed to do this? (From My Best Mathematical and Logic Puzzels by Martin Gardner, Puzzle 5, “Scrambled Box Tops”.)
This was a nice challenge, not too hard and kept all of us engaged. The temptation to pick in the box or get both marbles out was a bit too much. It worked best when three people were hiding the marbles one in each hand.
7 October 2017: Electro-Dough
Add some salt (and lemon juice) to dough, and it conducts! Let’s make some circuits.

|

|
23 September 2017: Weight Puzzle
There are twelve balls, eleven are the same, but one has a different weight from the others. How can you find the ball with the different weight using the minimum number of scale weighings?

|

|

|
16 September: Mirror Symmetry
What is the next image in the pattern?

9 September: The Farmer, the Fox, the Goose, and the Grain
The farmer has a fox (who will eat the goose), goose (who will eat the grain), and grain to bring back from the market in a boat that can only carry one at a time. How can the farmer get everyone safely to shore?

|

|

|

|
26 August 2017: Eclipse
On August 21 there was a total solar eclipse for parts of the US, and a near-total solar eclipse for Charlottesville. For the next math club, we wanted to understand what an Eclipse was, and why they are so rare.

The big purple ball represents the sun.
| Radius of Sun | 432288 miles | Distance from Sun to Earth | 93 million miles = 215 sun radii |
| Radius of the Earth | 3959 miles | Earth radii to Sun | 23,480 |
| Radius of the Moon | 1079 miles | Distance from Earth to Moon | 239,800 miles = 60.5 earth radii |
So, to represent the Earth we need something roughly 1/109 the radius of the sun. For the big purple ball, which has radius about 10 inches, we needed something with radius 0.1 inches — a small marble was the closest readily available, but with its blue and green swirly color made an excellent earth. The moon, 1/3 the radius of the earth, was a small piece of fuzz.
Scaling the size of the Sun down to the big purple ball, means the distance to the earth (normally 93 million miles) would scale down as 1 inch = 43228 miles. This mean the earth should be 179 feet away from the sun, and the moon would be 5.5 inches from the earth.

|

|
It actually worked! If you held the moon (fuzz) in just the right place, it would just occlude the sun.

We will be ready for the next eclipse in 2024!
13 April 2017: Egg Coloring

|

|
16 March 2017: Polygons

|

|
9 March 2017: Shadowy Similar Triangles

|
Let's use our shadows to measure its shadow!  Opps...it goes across the street. We'll have to try again closer to noon. |
2 March 2017: Viral Fishy Stories
(Inspired by Tiddler: The Story-Telling Fish)
How long does it take for a story to spread across the ocean? What if everyone tells the story to just one person? What if everyone tells the story to two new people? (We don’t have enough fish, but enough stuffies to get through 6 stages!)

|

|

(No pictures of actual math for this one, but lots of jumping in luggage!)
23 February 2017: Crazy Calendars
Calendars are puzzles - the last day of this month, first with the first day of the next month. There are different shapes of months because the number of days is either 30 or 31, and February is really odd.

|

|

Lucky for us, everyone’s birthday is between today and the end of June!
(Charlotte and Dorina are fighting over the June 29 square.)
Calendars (Excel spreadsheets, to print, use landscape mode and scale-to-fit): 31-day months, 30-day months
3 December 2016: Hamiltonian Cycles!
Find a path that starts from the castle and visits each character once, but cannot use any road more than once.

[PowerPoint]
24 September 2016: Ruling Rulers

|

|
28 August 2016: Trying Triangles

Can you make a triangle with any three sticks? Also, tracing the angles of any triangle to see they make a line!
21 August 2016: Circles and Ellipses
Drawing circles and ellipses with a string around thumbtacks on a board.
24 July 2016: Water Ballistics

17 July 2016: Shadow Monsters
 |

|
 |

|
Inspired by The Gruffalo’s Child, we saw who could make the biggest shadows.
9 April 2016: Double Dice Probabilities

|

|
26 March 2016: Fibonacci Bunnies!

Can’t have an Easter weekend meeting without lots of bunnies!
Mommy Bunny ⇒ Mommy Bunny and Baby Bunny
19 March 2016: Set Theory: Unicorns, Pegasi, and Alicorns

|

|
5 March 2016: Transitivity!

Balancing is transitive!
27 February 2016: Commutativity!

Mixing water colors is commutative! This means we end up with the same color when we mix the same colors, regardless of the order in which they are mixed. Mostly, though, we eventually end up with a murky, greenish-purple color after enough colors are combined.














